研究紹介

「ダイアモンドにおける励起子多体束縛状態の安定化機構の理論的解明」

　光子の吸収により半導体中に励起された電子と正孔は、Coulomb力により束縛し励起子と呼ばれる準粒子を形成することがある。 シリコンやダイアモンドのような半導体では、電子と正孔は正負の単位電荷を持った独立粒子として上手く記述できるため、励起子は水素原子の固体中での類似物となっている。 励起子は互いに結合し、より複雑な複合粒子を形成することが知られている。 励起子分子やトライオン(励起子+正孔、励起子+電子)はそのような束縛状態の例であり、励起子と合わせ固体の光学応答を理解する上で重要な存在である。

　電子正孔少数体系の束縛限界がどこに存在するかという問いへの答えは明らかになっていない。水素原子やポジトロニウムの三体束縛状態が存在しないことから、電子・正孔の有効質量比の広い領域で励起子の三体束縛状態も不安定であることが予想される。 これに対し、WangとKittelは間接ギャップ半導体中では縮退したバレーとバンドの自由度が同一粒子間のPauli斥力を緩和し、励起子N体束縛状態(Polyexciton(PE_N))が安定化される可能性を指摘した[1]。 一方で、Omachiらはダイアモンドの発光スペクトル中で自由励起子の発光崩壊よりも低いエネルギー領域に一連のピークを観測し、 それらはPE_N(N≤6)内部での励起子発光崩壊に由来するものと解釈した[2]。

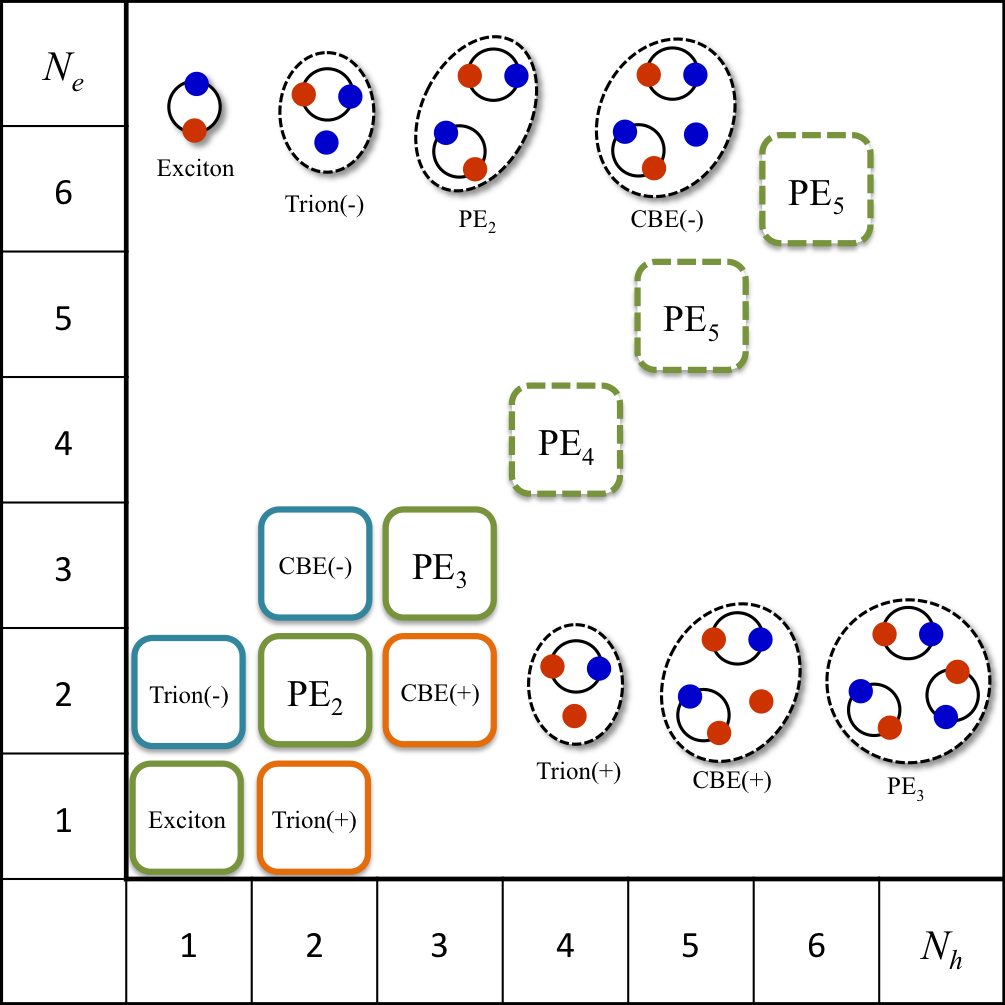
　我々のグループは電子正孔量子少数体系のSchrödinger方程式を直接解くことで、ダイアモンド中のPE_Nの安定性の数値シミュレーションによる検証を行った。 電子正孔系は多重バレー・バンド自由度と有効質量異方性を取り込んだHamiltonianにより記述される。 波動関数はCorrelated Gaussian基底により表現した。 この基底は粒子間相対座標に露わに依存し、Hamiltonianの行列要素を解析的に評価でき多重積分を必要としない[3]。 我々の数値計算はPE₂、PE₃に加え、トライオンや荷電励起子分子(Charged Biexciton、図中のCBE)の安定化を明らかにした。 電気的に中性な複合粒子の束縛エネルギーは実験値を定量的に再現し、我々はPE_Nの存在についての40年来の議論に対して数値計算の面から安定性を示すことに成功した[4]。

 

[1] J. Wang and C. Kittel, "Excitonic Molecules: A possible new form of chemical bonding ", Phys. Lett. 42A, 189(1972).

[2] J. Omachi, T. Suzuki, K. Kato, N. Naka, K. Yoshioka, and M. Kuwata-Gonokami, "Observation of Excitonic N-Body Bound States: Polyexcitons in Diamond", Phys. Rev. Lett. 111, 026402(2013).

[3] J. Mitroy, S. Bubin, W. Horiuchi, Y. Suzuki, L. Adamowicz, W. Cencek, K. Szalewicz, J. Komasa, D. Blume, and K. Varga, "Theory and application of explicitly correlated Gaussians", Rev. of Mod. Phys. 85, 693(2013).

[4] H. Katow, J. Usukura, R. Akashi, K. Varga, and S. Tsuneyuki, "Stability of excitonic complexes in a multi-valley/band semiconductor", APS March Meeting 2016, Baltimore, paper in preparation.

---