Tsuneyuki Research Group

Research

"Theoretical investigation of the stability of excitonic N-body complexes in diamond"

A photoexcited pair of electron and hole in semiconductor forms a quasiparticle called exciton by the attractive Coulomb intraction. In semiconductors like silicon or diamond, electrons and holes are well described as independent particles with negative or positive unit charge, hence the exciton can be regarded as an analogy of hydrogen in condensed matters. It is also known that excitons combine to form more complicated complexes. The excitonic molecules (or biexciton) and trions (exciton+electron, exciton+hole) can be given as well known examples. These fundamnetal bound states are essential to understand optical responses of solids.

It is difficult to answer that how many bound states of electrons and holes can exist. By considering the instability of triatomic hydrogen and positronium trimer, we can expect that the excitonic three-body complexes are unstable in wide range of the electron-hole effective mass ratio. However, Wang and Kittel pointed out the possibility of the formation of excitonic N-body bound states (polyexciton, PE_N) in indirect gap semiconductors due to the relaxation of the Pauli repulsion by degenerate valley and band degrees of freedom[1]. Omachi et al. recently reported their experimental observations of a series of peaks energetically below the peak of free exciton recombinations in photoluminescence spectrum of diamond, and they attributed those peaks to exciton recombinations inside PE_N(N≤6)[2].

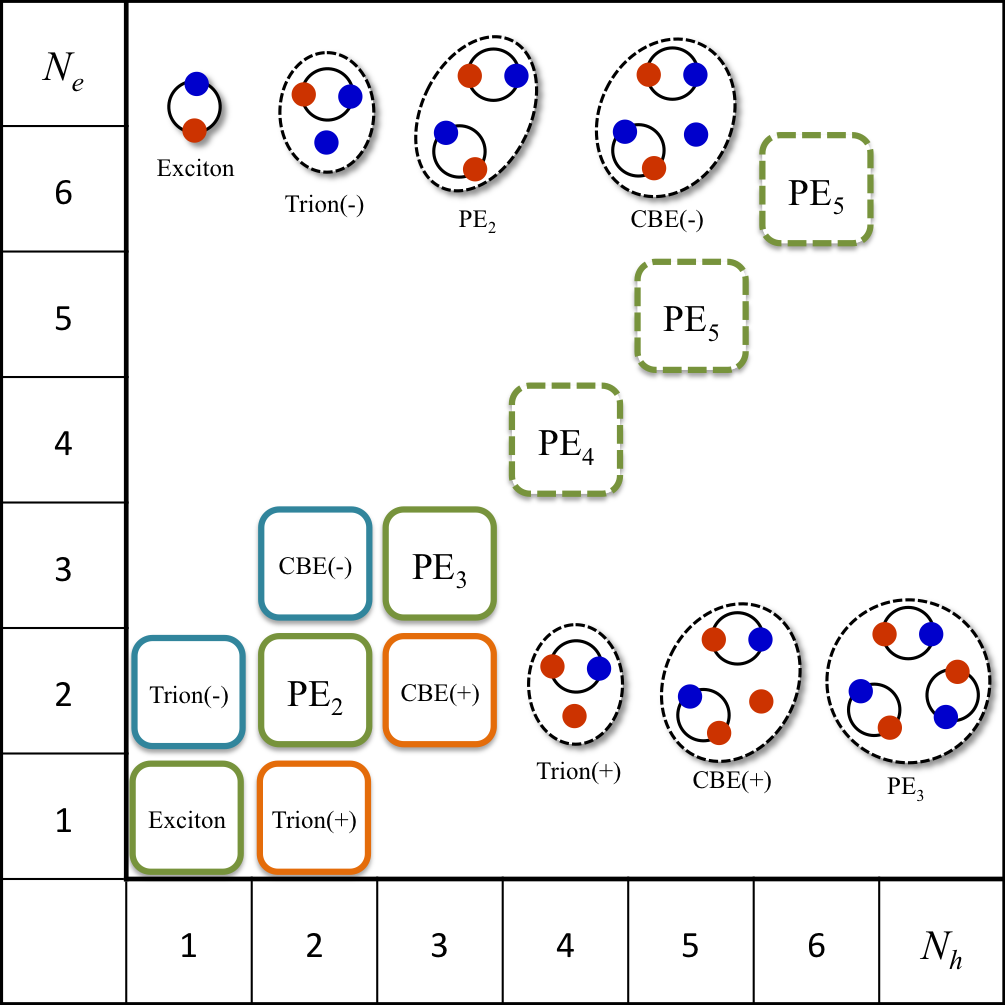
Our group investigated the stability of PE_N in diamond numerically by solving the Schrödinger eqation of the electron-hole quantum few-body system. The electron-hole system in diamond is described by a Hamiltonian including the effects of multiple valley and band degrees of freedom and effective mass anisotropy. The trial wave function is expressed by the explicitly correlated Gaussian (ECG) basis. The ECG basis explicitly depends on the relative coordinates beween particles and enables us to calculate matrix elements of Hamiltonian completely analytically[3]. Our study revealed the stability of PE₂, PE₃, trions, and charged biexcitons (CBE). Binding energies of neutral bound states quantitatively reproduce the experimentally observed values and we succeeded to provide numerical evidence of the stability of PE_N against the 40 year-long controversy of the presence of PE_N[4].

[1] J. Wang and C. Kittel, "Excitonic Molecules: A possible new form of chemical bonding ", Phys. Lett. 42A, 189(1972).

[2] J. Omachi, T. Suzuki, K. Kato, N. Naka, K. Yoshioka, and M. Kuwata-Gonokami, "Observation of Excitonic N-Body Bound States: Polyexcitons in Diamond", Phys. Rev. Lett. 111, 026402(2013).

[3] J. Mitroy, S. Bubin, W. Horiuchi, Y. Suzuki, L. Adamowicz, W. Cencek, K. Szalewicz, J. Komasa, D. Blume, and K. Varga, "Theory and application of explicitly correlated Gaussians", Rev. of Mod. Phys. 85, 693(2013).

[4] H. Katow, J. Usukura, R. Akashi, K. Varga, and S. Tsuneyuki, "Stability of excitonic complexes in a multi-valley/band semiconductor", APS March Meeting 2016, Baltimore, paper in preparation.