研究紹介
「高効率なブリルアン領域積分法の開発」
固体における量子力学に基づくシミュレーションを行い、 全エネルギー、力、電荷密度、状態密度、応答関数、フォノン振動数などのあらゆる量を計算するときに 共通してあらわれる演算のひとつとしてブリルアン領域積分がある。 これは、ブリルアン領域全体、もしくはその一部(占有領域、非占有領域、等エネルギー面上など)のブロッホ軌道からの寄与を 数値的に積分するものである。 この演算をいかに効率よく、すなわち少ない計算コストで精度よく行うかという事は 固体における数値計算に共通する問題である。
しかし、この積分はしばしば数値的に取り扱いづらいものとなる。
たとえば金属の占有領域が積分範囲となる場合、それはフェルミ面の内側として定義され、
一般的に非常に複雑な形状となる。
このような場合には、次のような手順で積分を行うことができる。
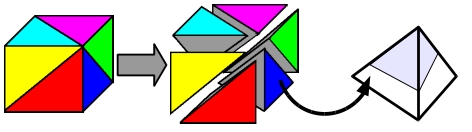
- 1, ブリルアン領域を一様なメッシュで分割する。
- 2, ひとつのメッシュを6個の四面体で分割する。
- 3, 四面体の各頂点での軌道エネルギーの値を調べることにより、 四面体内部の占有領域を切り取ることができる。
計算を効率的に行うためには、なるべく粗いメッシュを用いて計算コストを下げながら、 かつ精度はメッシュが細い時と同じくらいに保つことが望ましい。 この目的のために我々は従来用いられてきたテトラへドロン法の改良に取り組んだ。 従来のテトラへドロン法ではメッシュが粗い時には、 四面体内部の軌道エネルギーを過大評価する。これによりメッシュが粗い時の誤差が増大する。 この過大評価は四面体内部で軌道エネルギーを線形補間することに由来する。 そこで我々は、軌道エネルギーの多項式補間を用いて四面体内部の占有領域を切り取る方法を考案した[1]。 また、この方法を第一原理計算パッケージQuantumESPRESSOに実装し[2]、 特に金属におけるフォノンおよび電子フォノン結合の計算においてそれが有効であることを示した。
[1] M. Kawamura, Y. Gohda, and S. Tsuneyuki, "Improved tetrahedron method for the Brillouin-zone integration applicable to response functions" Phys. Rev. B 89, 094515 (2014).
[2] http://qe-forge.org/gf/project/dfpttetra/