Tsuneyuki Research Group

Research

"Development of an efficient Brillouin-zone integration method"

When we calculate any quantities in solid (total energy, force, charge density, response function, phonon frequency, etc.) through a quantum mechanical simulation, we have to perform the Brillouin-zone integration. In this integration, we integrate numerically contributions from Bloch states in whole Brillouin zone or in part of that (occupied region, unoccupied region, isoenergy surface, etc. ). It is a common problem in the computational material science how we perform efficiently (low numerical costs and high accuracy) this integration.

However, sometimes this integration becomes difficult for the numerical calculation. For example, when integrated region is the occupied region in a metal, it becomes the inside region of the Fermi surface whose shape is very complex. In this case, we perform this as follows:

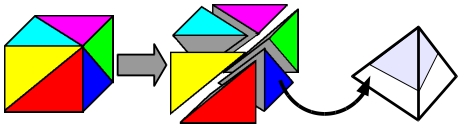
1. 1, We divide the Brillouin zone by using an uniform mesh.
2. 2, Each cells are divided into six tetrahedra.
3. 3, Comparing the Fermi energy and the orbital energy at corners of the tetrahedron, we trim occupied region from the tetrahedron.

This method is called the tetrahedron method. A similar procedure is used to display isosurface in the computer graphics.

We may reduce the numerical cost by using a coarse integration mesh while keeping the accuracy as high as we use a dense integration mesh. For this purpose, we improve on the tetrahedron method. When we use a coarse integration mesh, the conventional tetrahedron method overestimates orbital energy in a tetrahedron. Therefore the error increase. This overestimation comes from the use of the linear interpolation of orbital energy in a tetrahedron. On the basis of this fact, we develop a method in which we can trim more precisely the occupied region in a tetrahedron by using the higher order polynomial interpolation. We implement this method to a first-principles electronic structure calculation package "Quantum ESPRESSO" [2] and demonstrate its efficiency in calculations of the phonon and the electron-phonon interaction in a metal.

[1] M. Kawamura, Y. Gohda, and S. Tsuneyuki, "Improved tetrahedron method for the Brillouin-zone integration applicable to response functions" Phys. Rev. B 89, 094515 (2003).

[2] http://qe-forge.org/gf/project/dfpttetra/

---