研究紹介
「トランスコリレイティッド法の波動関数を用いた拡散量子モンテカルロ法」
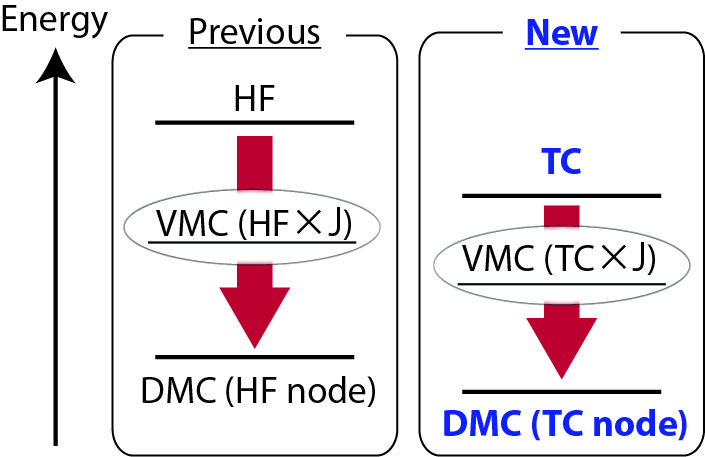
拡散量子モンテカルロ法(DMC)は高度に電子相関を取り込める第一原理電子状態計算手法であり、計算コストのスケーリングが良いことから、特に固体において信頼できる電子状態計算手法として用いられている。しかし電子系の計算では多体波動関数の節を固定する節固定近似を用いる必要があり、得られる電子状態の精度は前もって用意した節の質によって決まる。多くの物質では用いる節によって構造や電子状態は変わらないとされているが、近年、遷移金属酸化物では節の質も重要であるとの報告がなされている。
こうした背景のもと我々はトランスコリレイティッド(TC)法の波動関数の節を用いたDMCの計算を行っている。TC法ではジャストロー因子により電子相関を露に取り入れた上で一電子軌道を最適化するため、TC法の波動関数はHF法の波動関数よりも良い節を持つことが期待される(右図)。
実際にTC法とHF法の波動関数を用いたDMCのエネルギーを比較することで、次の結果が得られた[1]。(1)短距離型の汎用的なジャストロー因子を用いるとTC法の波動関数の節はHF法の波動関数の節よりも良い、(2)電子ガスの解析で得られる長距離型のジャストロー因子を用いると、ギャップの小さい系ではTC法の節の方が良くなる。これらの結果はTC法の波動関数のDMCにおける有用性を示唆するものである。
[1] Y. Yamamoto, R. Maezono, M. Ochi and S. Tsuneyuki, in preparation.
< BACK >