研究紹介
「波動関数理論に基づく電子状態計算手法Transcorrelated法の開発」
現在の物理学を支える理論体系である量子力学に従ってSchrödinger方程式を解くことで、 原理的にはあらゆる物質の電子状態を求めることができる。 しかし、分子や固体のような多電子系において、 このSchrödinger方程式を厳密に解くことは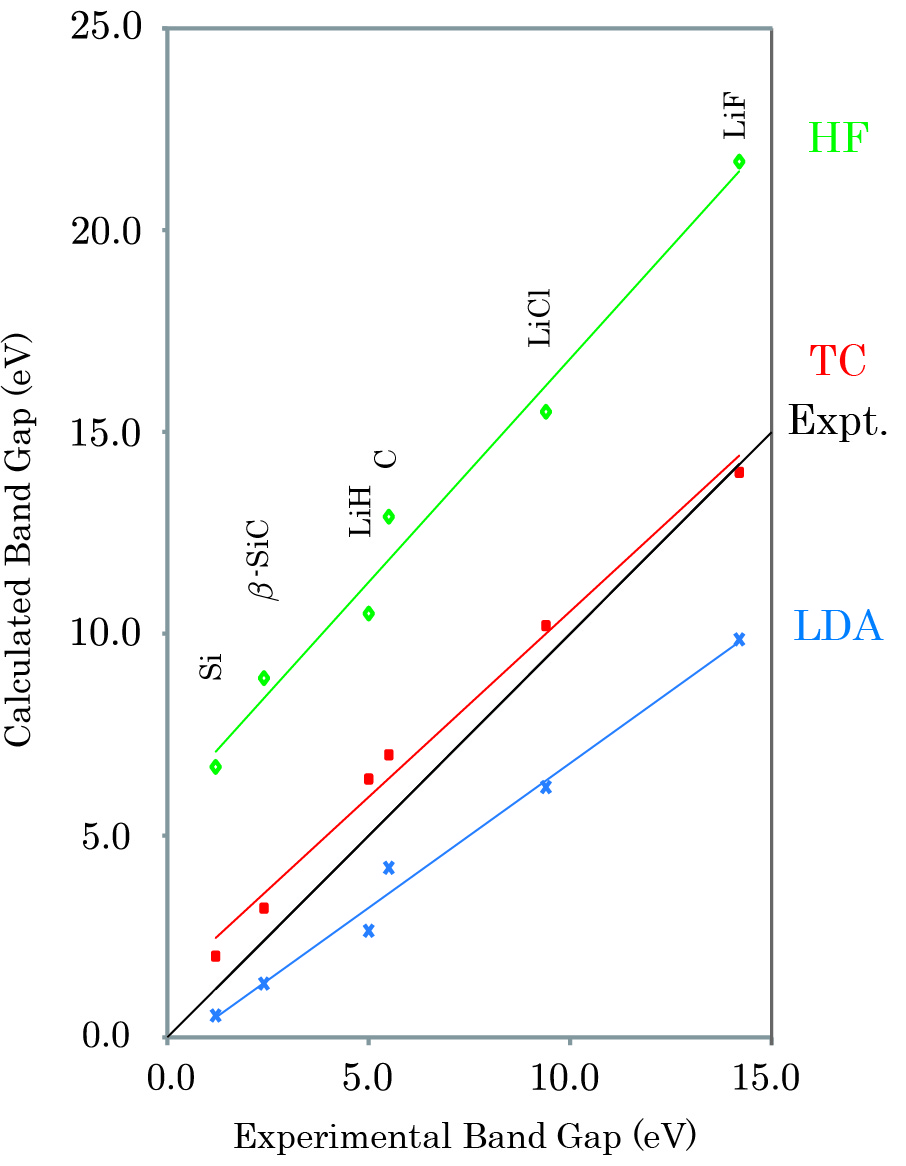 
ほとんど不可能である。そこで、近似的にしかも精度良く解く方法を開発することが重要な課題となる。
本研究では、固有方程式を相似変換してもその固有値は変わらないことを利用して、電子相関効果を担うJastrow因子によってSchrödinger方程式を相似変換する。 こうすることで、電子相関効果をHamiltonianに有効的に取り込めるため、 Hartree-Fock法と同じようにSlater行列式を試行関数としても比較的精度の高い計算が実行できる。この手法はTranscorrelated法と呼ばれており、我々のグループでは、現在までに原子・分子[1]、一様電子ガス[2,3]、固体[3]、モデル系[4]と幅広く本手法を適用し、その有用性を確認してきた。最近行ったアルゴリズムの改善[5]により、電子数に対してHartree-Fock法と同じスケールでの計算が可能となり、Jastrow因子の改善[6]、電子励起状態の光吸収スペクトル計算[7]や多体摂動論との組み合わせ[8]も可能となった。
本手法の特徴のひとつに、多体波動関数を露に扱うにも関わらず、電子相関の考慮された一電子エネルギースペクトルが得られることが挙げられる。特に固体ならばバンド図を描くことが出来る。図は、本手法によって計算された様々な固体のバンドギャップの値であり、Jastrow因子によって計算結果に大きな改善が得られることがわかる[6]。
[1] N. Umezawa and S. Tsuneyuki, "Transcorrelated method for electronic systems coupled with variational Monte Carlo calculation", J. Chem. Phys. 119, 10015 (2003).
[2] N. Umezawa and S. Tsuneyuki, "Ground-state correlation energy for the homogeneous electron gas calculated by the transcorrelated method", Phys. Rev. B 69, 165102 (2004).
[3] R. Sakuma and S. Tsuneyuki, "Electronic Structure Calculations of Solids with a Similarity-Transformed Hamiltonian", J. Phys. Soc. Jpn. 75, 103705 (2006).
[4] S. Tsuneyuki, "Transcorrelated Method: Another Possible Way towards Electronic Structure Calculation of Solids", Prog. Theo. Phys. Suppl. 176, 134 (2008).
[5] M. Ochi, K. Sodeyama, R. Sakuma, and S. Tsuneyuki, "Efficient algorithm of the transcorrelated method for periodic systems", J. Chem. Phys. 136, 094108 (2012).
[6] M. Ochi, K. Sodeyama, and S. Tsuneyuki, "Optimization of the Jastrow factor using the random-phase approximation and a similarity-transformed Hamiltonian: Application to band-structure calculation for some semiconductors and insulators", J. Chem. Phys. 140, 074112 (2014).
[7] M. Ochi and S. Tsuneyuki, "Optical Absorption Spectra Calculated from a First-Principles Wave Function Theory for Solids: Transcorrelated Method Combined with Configuration Interaction Singles", J. Chem. Theory Comput. 10, 4098 (2014).
[8] M. Ochi and S. Tsuneyuki, "Second-order Møller-Plesset perturbation theory for the transcorrelated Hamiltonian applied to solid-state calculations", Chem. Phys. Lett. 621, 177 (2015).